

La deducción es el procedimiento por el cual obtenemos información a través de otra información, es decir, obtenemos conclusiones a partir de premisas.



Galileo Galilei, quien usó el método de la deducción, afirmó después de sus observaciones con el telescopio que:
-Todos los planetas son redondos
-La Tierra es un planeta
-Seguramente la Tierra es redonda

Con este método la ciencia ha llegado a conclusiones fundamentales para la humanidad.
Otro método para determinar la validez de los argumentos deductivos, y en el cual ya no se aplican valores de verdad, es el de las reglas de inferencia.

Una regla de inferencia es un argumento que siempre es válido y que se expresa en estructuras simples que no cambian, independientemente del contenido.
Las estructuras en las reglas de inferencia son como moldes que pueden ser llenados de distintas sustancias, por ejemplo el molde puede llenarse de gelatina, de mousse de atún o de budín de pan.


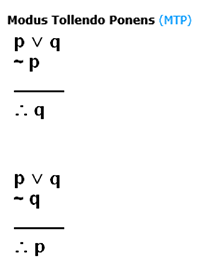
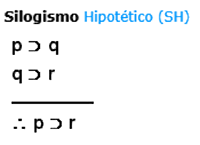
A continuación te presentamos las estructuras de las reglas de inferencia con las que trabajaremos, con su respectiva abreviatura. Observa la estructura y la imagen y reflexiona acerca de cómo se relaciona una con otra.
Hay reglas que tienen dos estructuras, cualquiera de ellas es una buena aplicación de la regla. Podemos usar una u otra, según lo necesitemos.




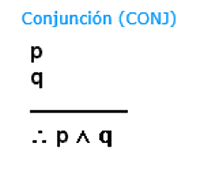

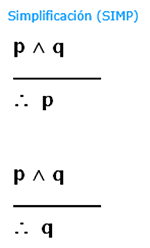

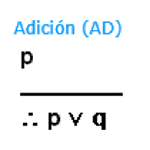


Es importante que ya poseas conocimiento de las conectivas lógicas, y de la lectura literal de un argumento. Por ejemplo, tomemos el MPP.
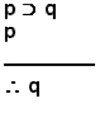
Cuya lectura literal sería la siguiente:
Si p entonces q
p
entonces, q
Pero no sólo nos interesa que sepas leer literalmente, sino que comprendas qué nos está diciendo la regla, pues eso nos permitirá una mejor aplicación del método para la solución de problemas y un mejor uso de dicha estructura en tu vida cotidiana. Para dicho fin a continuación te pedimos realices la siguiente actividad.

Sigue las instrucciones paso a paso:
Descarga el cuadro para que realices la actividad dando clic en el botón: description"Lectura literal y parafraseo"
Escribe la lectura literal o el parafraseo según sea el caso de cada regla de inferencia presentada.
Recuerda que parafrasear es explicar con tus propias palabras cómo entiendes la regla. Te damos un ejemplo para que te quede más claro.

Parafraseo: La regla nos dice que dados dos elementos si están unidos a través de una “y”, entonces podemos obtener como conclusión cualquiera de sus dos miembros.
Compara tu actividad con el cuadro de respuestas: description"Respuestas de Lectura literal y parafraseo"

En esta actividad tienes que distinguir a qué tipo de regla pertenece cada argumento.
1. El puma y el leopardo son felinos, por lo tanto el puma es un felino.
2. Si voy a tu casa, entonces pierdo mucho tiempo. Si pierdo mucho tiempo, entonces no termino la tarea. Por lo tanto, si voy a tu casa, entonces no termino la tarea.
3. Tus acciones me hacen pensar dos cosas: eres ingenua o eres muy tolerante. Sé que no eres muy tolerante. Por lo tanto, eres ingenua.
4. Ganas el premio. Ganas el premio o me muero.
5. Si existiera Dios, entonces no habría mal en el mundo. Hay mal en el mundo. Por lo tanto Dios no existe.

En la actualidad los procesos de producción y el deterioro ambiental son problemáticas a nivel mundial, como la destrucción de la capa de ozono, el calentamiento global, la pérdida de biodiversidad, el cambio climático y los residuos tóxicos, los cuales afectan a todo el planeta.
Por otra parte la imagen y apariencia de juventud, salud y bienestar es actualmente una situación que se manifiesta como una exigencia sociocultural para los habitantes de todo el mundo. Ello crea la necesidad de generar gran cantidad de productos de alto consumo, lo cual contribuye al deterioro ambiental. Esta problemática plantea la necesidad de buscar una solución que integre producción, consumo y cuidado del medio ambiente, lo cual representa un reto de acción global.

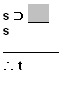
Escribe el elemento faltante en el espacio de escritura, de acuerdo a las reglas de inferencia que practicamos anteriormente.
Cuando hayas concluido, da clic en el botón comprobar.
 |
|
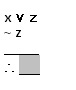 |
|
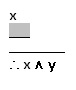 |
|
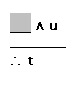 |
|
 |